Common Core Math vs. Old School Math

A couple of nights ago, NHL came home and began to do his homework.  As he did his math work, he began to get agitated.  Soon, he was in full-blown panic mode.  He was doing decimal division and didn’t know how to do it.  The method that they were being taught was confusing to him.

The problem that he was given was 1.62 / 0.27.  First, I’ll use the Common Core method that NHL was given as illustrated by this photo:

Do you understand how to do this now?  No?  Well don’t worry.  Neither did I.  After a day of thinking about it, I finally figured it out.  You draw a picture showing tenth segments totaling 1.6.  Next, you separate these out into groupings of 4 tenths segments (0.4).  Finally, you count the number of groups and you get your answer (4).

Going back to the original problem (1.62 / 0.27), you’d draw a picture like this:

(Where each line represents one hundredth.)

Next, you would separate these out into groupings of 27 hundredths.

Finally, you would count the number of groups and get the answer: 6.

I find two problems with this method.  First of all, you aren’t learning to actually work with the numbers.  You aren’t figuring out how to actually divide one number into another number.  Secondly, this quickly breaks down as you get to larger numbers.  If this problem involved the number 1.621, would you force the kids to draw 1,621 thousandths lines?  Would dividing 16.215 mean needing to draw over 16,000 lines?  At what point does the child learn to actually work with the numbers?

Now, let’s compare this to how I learned to do decimal math (“Old School Math”).

First step is to write out the problem like so:

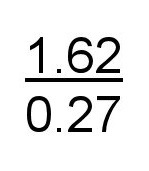
Next, multiply the top and bottom by 100 to get rid of those pesky decimal places.  (100/100 = 1 so you aren’t changing the number.)

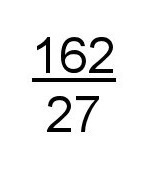
Now, you can break up 27 into numbers that, when multiplied together make 27.  1*27 wouldn’t be any help, but 3*9 would be.  You can also go one step further and break up the 9 into 3*3.  So now you have:

Now just divide the 162 by each of the threes.  The first one gives you:

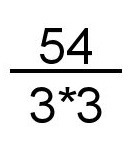
The second gives you:

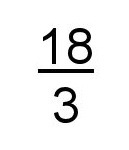
And finally, you come up with the answer: 6.

This method is much more scalable – you don’t need to write out a thousand lines to represent a number – and actually makes the student deal with the numbers.

When I showed this method to NHL, he understood it immediately and was able to solve the problem quickly.  Sadly, thanks to New York State’s implementation of Common Core, the teacher isn’t allowed to change her methods to suit the children.  Neither are the kids allowed to use alternative methods to solve problems.  If NHL is given 1.62/0.27 on a test and he solves it via the “Old School” method, he will be marked wrong.  Even if he gets the right answer, he will be told he’s wrong because he didn’t use the Common Core Approved method.

This course of action will just teach students to think INSIDE the box and that deviating from the set path is the wrong thing to do – instead of something that might result in a fantastic discovery.  Common Core Math will wind up turning many students off of math.  As a math geek, that makes me very sad.  I worry about NHL and his peers and their future education.