Extreme Geekery: Jupiter Jump
 Did you hear the amazing news? If you jump on the right day, a planetary alignment of Jupiter and Pluto will cause a decrease in gravity and you will be able to float in the air for five minutes! It’s definitely true because I read it on the Internet.
Did you hear the amazing news? If you jump on the right day, a planetary alignment of Jupiter and Pluto will cause a decrease in gravity and you will be able to float in the air for five minutes! It’s definitely true because I read it on the Internet.
Ok, you’ve got me. This isn’t true. Not in the least. It’s 100% grade-A hokum. Phil Plait, aka The Bad Astronomer, has debunked this more thoroughly than I could. It did make me wonder though: What would it take to float in the air for five minutes? How much would we have to alter the Earth’s gravity in order to accomplish this feat? Or, likely more accurate to the “Zero G Day” myth, how close or massive would Jupiter need to be to accomplish this? Consider this a cosmic equivalent to the Mythbusters’ replicating the results.
We can think of a jump using this diagram.
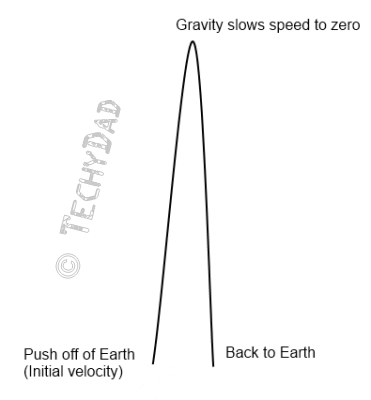
First, our legs push off of the Earth with an initial velocity. Next, the Earth’s gravity decelerates us bit by bit until we reach the top of our jump where our speed becomes zero. Finally, gravity’s acceleration pulls us back down to Earth. (In reality, you might need to calculate other items like air resistance, but we’ll simplify matters and ignore the air for now.)
Since the top of our jump is halfway through it, let’s further simplify matters by not calling this a five minute jump that we are going to attempt. Instead, we’ll say that it takes gravity two and a half minutes to slow our initial push-off speed to zero.
Let’s start with a normal jump, though. Go ahead and jump. If you are like me, you went up and came back down in about a third of a second. There’s an easy equation we can use to calculate acceleration (or deceleration) over time:
vf = vi + a*t
In other words, the final speed is equal to the initial speed plus the product of acceleration (in this case, gravity) and time.
We don’t know the initial speed, but we do know the time (half of a third of a second, or about 0.167 seconds), the deceleration (-9.8 meters per second2), and the final speed (zero). This gives us:
0 = vi – 9.8*(0.167)
or
vi = 1.617
That’s the initial velocity that our legs have provided us. But what about our “Zero G Day” jump? How small would gravity need to be to allow us to push off with the same force and decelerate to zero in 2.5 minutes?
Again:
vf = vi + a*t
This time, we know vf (zero again), vi (1.617 from the previous example), and t (2.5 minutes, which is 150 seconds). This gives us:
0 = 1.617 + 150a
or an acceleration of -0.01078 meters per second2. Given that normal Earth gravity is 9.8 meters per second2, this would be a mere 0.0011g.
How small is 0.0011g? Well, according to the Planetary Fact Sheet from NASA, if you were walking on the surface of the Mercury, you’d experience 0.378g. Maybe we need something smaller like our Moon? 0.166g. Let’s go to dwarf planets and look at Pluto. 0.059g. We still haven’t gotten to our “Zero G Day” gravity figure. Even Pluto has over 53 times the gravity we’re looking for. We might have luck with one of the smaller asteroids, but it would be a difficult search.
Clearly, were Zero G Day to actually occur, this would be a major disruption. The effects wouldn’t simply be limited to a cool jump. But what could cause such a thing? As Phil Plait pointed out, Jupiter – as massive as it is – doesn’t influence us enough gravitationally. This is because gravity decreases as objects get more distant. Specifically:
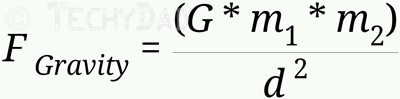
G is the universal gravitational constant or 6.673 x 10-11 N m2/kg2. This isn’t to be confused with “little g” which stands for the gravity on Earth. Don’t worry if you are a bit confused, though, as you’ll see, G isn’t going to matter much.
When you jump in our hypothetical “Jupiter Has Much More Gravity” situation, Jupiter pulling up almost as much as the Earth is pulling down.
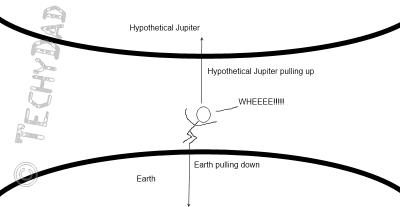
In fact, we could say that the force of Jupiter pulling you up is equal to 0.9989 times the force of Earth pulling you down. (Thus giving us the 0.0011 Earth gravity left over.)
Since we have the force equation from before, we can express this as:

Since G and m1 are both on each side, we can eliminate those:

Plugging in the values for the Earth’s mass (5.98 x1024kg) and distance (6.38 x 106 km) gives us:

or:

Bringing Jupiter’s distance to the other side gives us:

Now we can either solve for distance or mass for Hypothetical Jupiter. Let’s do one and then the other. First, we’ll assume that Hypothetical Jupiter is in its current orbit and will calculate how massive it would need to be. Next, we’ll keep Jupiter as massive as it is right now and just move it as close to the Earth as it would need to be.
Plugging in Jupiter’s minimum distance from the Earth – 588.5 * 106 (source: NASA), we get a mass of 509,108.4 * 1029 kg. That same website gives the real Jupiter’s mass as being 1,898.3 * 1024 kg. So Hypothetical Jupiter would need to be 26.8 million times as massive as Real Jupiter. This is much more massive than the Sun is (1,989,100 * 1024 kg). Almost 25,600 times as massive, in fact. This would make our Hypothetical Jupiter, more massive than any star we know of. Perhaps this would even be massive enough for Hypothetical Jupiter to collapse into a black hole.
On the other hand, we could keep Jupiter the same size and just move it closer to the Earth. Solving for distance, we get this equation:

With Jupiter’s mass (1,898.3 * 1024), this gives us a distance of a distance of about 113,600 km. At first glance, this would appear to put Jupiter less than a third of the distance between the Earth and the Moon (384,400 km). Actually, though, it’s closer than that. You see, the distance is measured as the distance to the center of Jupiter. Jupiter has a radius of about 70,000 km so this would actually make Jupiter only 43,600 km from the Earth. This would be only 11% of the Earth-Moon distance and would be a mere 8,000 km from satellites orbiting in geostationary orbit.
At that distance, our Hypothetical Jupiter would not only let us stay aloft for 5 minutes, but would also pour tons of lethal radiation over the Earth. Not only that, but the Earth would probably be torn apart and fall into Jupiter.
In short, be glad that you can’t jump and stay aloft for five minutes. If you ever find yourself able to do this, you might not be around for long to enjoy your air time.
NOTE: The Jupiter image above is from NASA.


