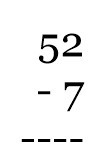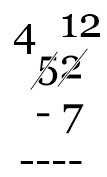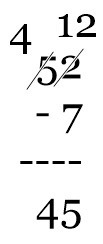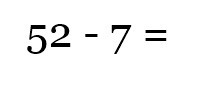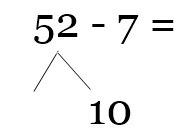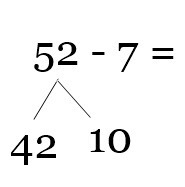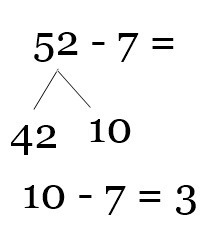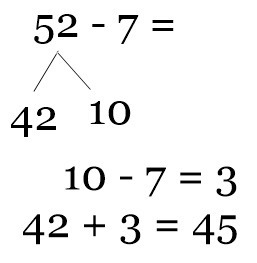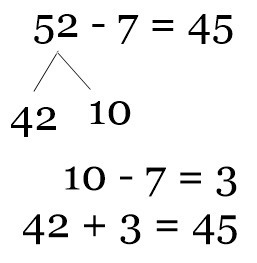Extreme Geekery: Giant Sun Birthday Cake
 Happy Birthday to me! Today I turn 41. Luckily, I’ll probably have a single candle on my cake (or two candles: a four shaped one and one shaped like the number one). I won’t have to deal with blowing out forty-one candles. Still, I began to wonder exactly how bright you could get with candles. Let’s suppose that the Sun was a giant birthday cake. How many candles would it need to keep outputting as much light as it currently does. (Since this is a thought experiment, we’ll ignore such mundane details as "How do the candles burn without an atmosphere" and "How do the candles not melt down with time".)
Happy Birthday to me! Today I turn 41. Luckily, I’ll probably have a single candle on my cake (or two candles: a four shaped one and one shaped like the number one). I won’t have to deal with blowing out forty-one candles. Still, I began to wonder exactly how bright you could get with candles. Let’s suppose that the Sun was a giant birthday cake. How many candles would it need to keep outputting as much light as it currently does. (Since this is a thought experiment, we’ll ignore such mundane details as "How do the candles burn without an atmosphere" and "How do the candles not melt down with time".)
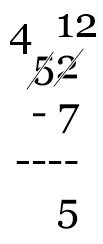
The Sun outputs about 6.84 x 1027 lumens. Written out, this is 6,840,000,000,000,000,000,000,000,000. That’s a LOT of lumens. The best reference I could find for a candle’s output was 12.56 lumens. Of course, the birthday candles I use tend to be smaller and so likely generate less lumans than other candles. Let’s round down to 10 lumens for a birthday candle. (Plus, this makes the math easier.)
If each candle is providing 10 lumans of light, we would need 684,000,000,000,000,000,000,000,000 candles. That’s 684 trillion trillion candles! I wonder if the warehouse stores carry ultra-mega packs of candles.
So we’ve got our candles and are ready to light them… Wait, first we need to put them in the cake. So we make a HUGE spherical cake and place the candles all around it. How big of a cake do we need? Well, if each candle has about 1 square centimeter of space around it (we’re packing them in), the cake would need a surface area of 684,000,000,000,000,000,000,000,000 square centimeters or 68,400,000,000,000,000 square kilometers. (That’s over 26,000,000,000,000,000 square miles.) The Sun itself has a surface area of 6.09 x 1012 square km. That’s a big cake!
How much bigger, you ask? Stand back, I’m going to use Math!
Now the surface area of a sphere can be calculated by pi*d2. Let’s say that the cake’s diameter is d1 and the Sun’s is d2. This gives us:
68,400,000,000,000,000 = pi*d12
and
6,090,000,000,000 = pi*d22
Obviously, the cake is some number, N, times bigger than the Sun so we can say:
d1 = N * d2
Plugging this into the first equation we get:
68,400,000,000,000,000 = pi*(N*d2)2
Or:
68,400,000,000,000,000 = pi*N2*d22
Now the second equation can also be written as:
d2 = square root(6,090,000,000,000/pi)
Plugging this into our calculations, we get:
68,400,000,000,000,000 = pi*N2*(square root(6,090,000,000,000/pi))2
Or:
68,400,000,000,000,000 = pi*N2*6,090,000,000,000/pi
The Pi’s cancel out and we can divide each side by 6,090,000,000,000 to get:
N2 = 1,123.15
This means that N is about 33.5.
Our birthday cake would need to be almost 34 times the size of the Sun just to be as bright as it is.
I think I’m going to need more frosting!
NOTE: The Sun Birthday Cake image above was made by combining Decorative Sun by ivak and Chocolate Birthday Cake(brown) by version2. Both images are available from OpenClipArt.org.


 Archimedes once said "Give me a lever long enough and a fulcrum on which to place it, and I shall move the world." He was waxing poetic about the power of the lever. The lever is one of several
Archimedes once said "Give me a lever long enough and a fulcrum on which to place it, and I shall move the world." He was waxing poetic about the power of the lever. The lever is one of several